Space-filling Curves and Their Applications

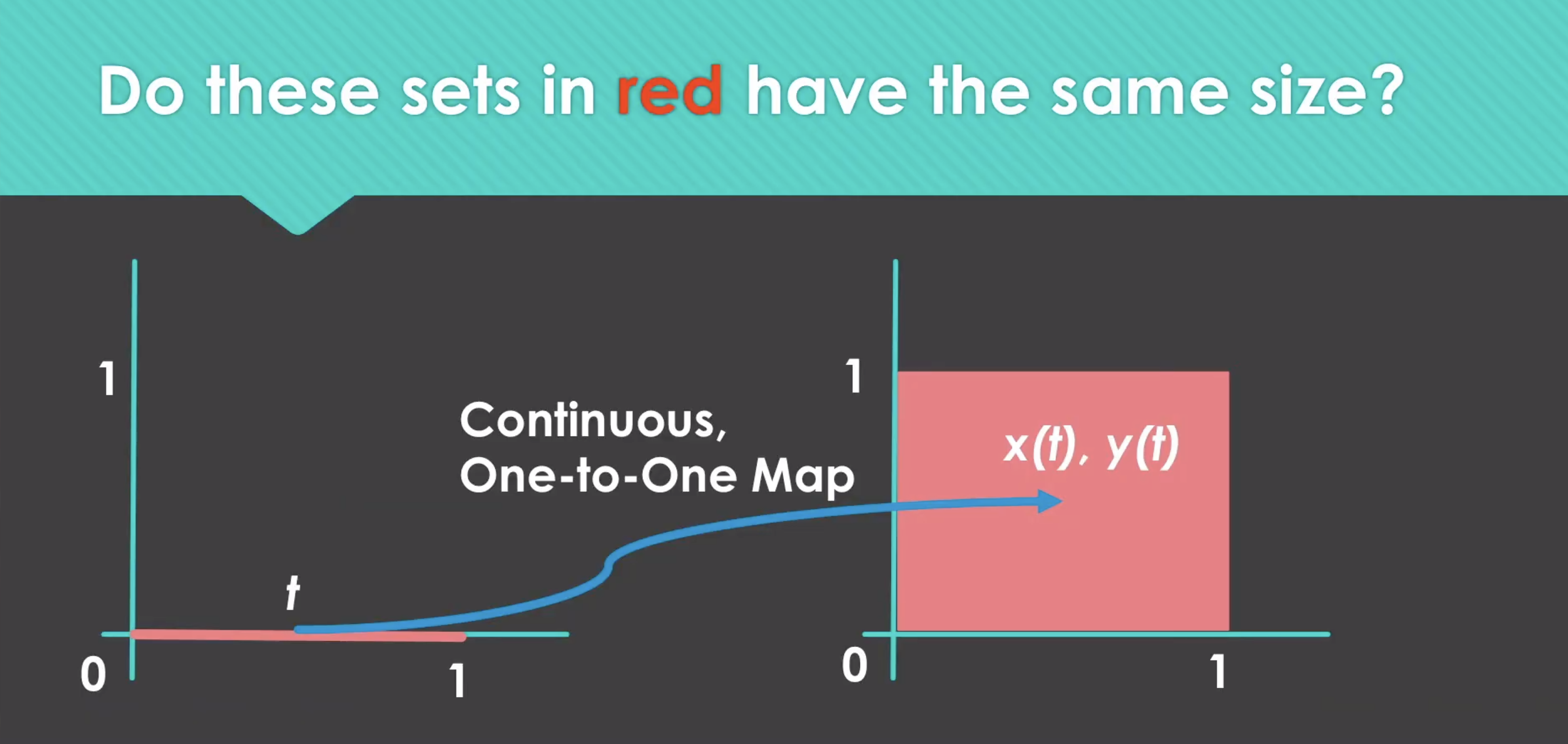
Prof Vincent Tan describes the concept of a space-filling curve, which is a strange mathematical oddity. Cantor showed that the set of points on the unit interval [0,1] has the same cardinality as that of the unit square [0,1]². Can we construct a continuous curve that maps from the unit interval onto the unit square? Prof Tan shows through an elementary construction of such a fractal that this is indeed possible. He also discusses some real-life applications of fractals in finance.

Modelling Epidemics with Networks

In curbing the spread of an infectious disease, the traditional focus is in understanding the disease itself and how the human body fights against infection. Dr Ng Kah Loon explains how mathematics surprisingly lends a helping hand in modelling the structure of the community in which the disease is spreading. Mathematical quantities, like the degree of clustering in a network, can provide insights to guide intervention strategies like quarantines and vaccinations.

Mathematics of Tsunamis

By using satellite radar ranging, it will be possible in the near future to detect disturbances on the surface of the ocean, anywhere on Earth. This will be extremely useful if it can be applied to detect tsunamis when they are still far from shore. Then there may be time to warn coastal populations, potentially saving tens of thousands of lives. Mathematical modelling of tsunamis allows us to predict the exact shape of the wave, given its speed. By correlating the shape and the speed, it may be possible to distinguish tsunamis from all of the other waves on the surface of the ocean, and so detect them.