Adaptive two-sample test for high-dimensional data

NUS statisticians have developed a simple and adaptive test for comparing two groups of high-dimensional data.
Testing the equality of the means from two groups of data is a fundamental inference problem. For high-dimensional data where the dimension of the data can be much larger than the total sample size, the classical tests either perform poorly or are not applicable. Several modifications have been proposed to address this issue. However, most of them are based on the asymptotic normality of the null distributions of their test statistics.

Prof ZHANG Jin-Ting from the Department of Statistics and Applied Probability, NUS and his former Ph.D. students have developed a simple and adaptive two-sample test which works well without the abovementioned requirement. The new testing method relaxes a key mathematical condition imposed in the literature, which guarantees the asymptotical normality of the existing test statistics. This key condition requires that the high-dimensional data are nearly uncorrelated. However, in real life, high-dimensional data is often highly or moderately correlated. This means that the existing tests are less useful when applied to high-dimensional data in a real world context.

The new test, on the other hand, is developed with the above key condition removed. The null distribution of the test statistic is approximated by a two-moment matched chi-square approximation. As the degree of freedom of the approximation chi-square distribution is consistently estimated from the data, the resulting new test can automatically adjust this parameter to the underlying covariance structure of the high-dimensional data. This means that the degree of freedom parameter can take small, moderate, or large values when the high-dimensional data is highly, moderately, or nearly not correlated. Numerical results show that the new testing method often performs better than existing methods for comparing the means of two groups of high-dimensional data of this nature.

Prof Zhang said, “The concept used in the proposed two-sample testing method can also be extended to other high-dimensional testing problems, including testing the equality of means for several groups of high-dimensional data and/or under unequal covariance structures.”

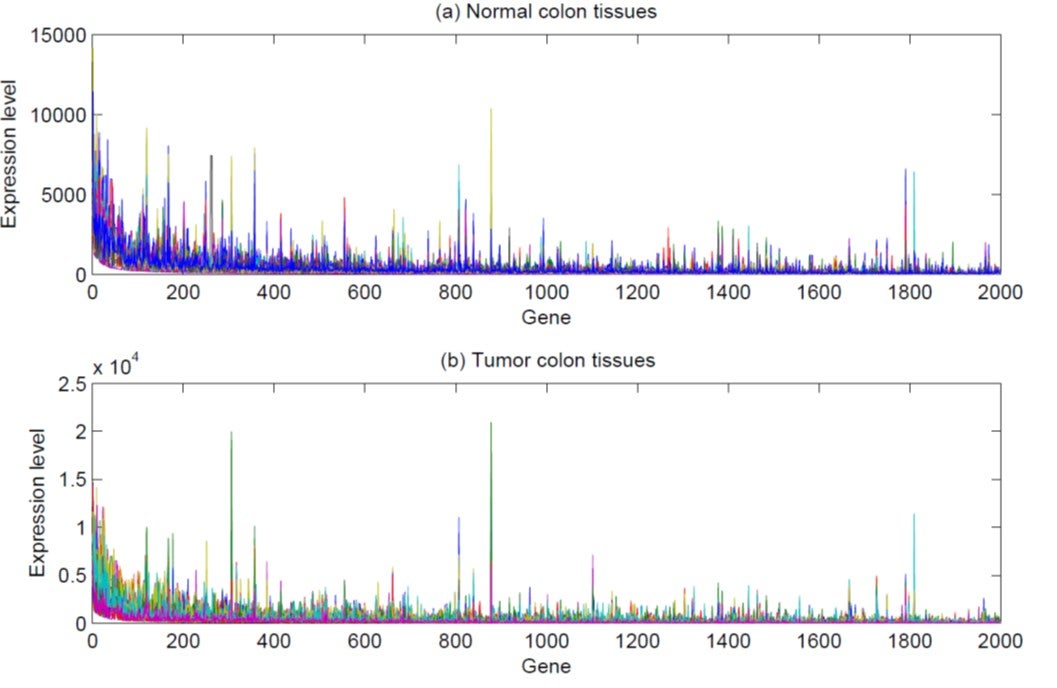
The figure demonstrates an application of the new two-sample test. The upper and lower panels display data obtained from 22 normal colon tissues and 40 tumour colon tissues respectively. Each of them have an expression level of 2000 genes. It is required to know if there is any difference in the gene expression levels between the normal and tumour colon tissues. Since the dimension of the data (2000) is much larger than the total sample size (62), it can be classified as a high-dimensional two-sample testing problem. Application of the new test to the above problem leads to a strong rejection of the null hypothesis, with a p-value of 0.000983. This means that statistically there is a difference in the gene expression levels. The estimated degree of freedom of the approximation chi-square distribution is about six, showing that existing methods which approximate their null distributions using normal distributions are biased and hence less accurate.

Reference:

Zhang JT*; Guo J.; Zhou B; Cheng MY, “A Simple Two-Sample Test in High Dimensions Based on L2-Norm”, JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION, DOI: 10.1080/01621459.2019.1604366. Published: 2019.