These algorithms are called “sequential Monte Carlo” (SMC) algorithms and have been used since the mid-90s. They can be highly effective in producing important statistical estimates, but often the algorithms require input information and expert knowledge to work well. They have been used for many applications, as described below. In these applications, the algorithms were used in situations where the input of the algorithms is adaptive, i.e. that input information is learnt by the algorithm. The issue is to show that these algorithms still return the correct integral; an unanswered question until [1].
The “adaptive” SMC algorithms have been used in many contexts; such as in finance [2] and genetics [3]. At the Risk Management Institute at NUS, it is used in the Credit research initiative http://www.rmicri.org/home/. This is a non-profit project using adaptive SMC for assistance in predicting credit risk rates. The website offers daily predictions from a probability of default model for about 60,400 listed firms in the Asia Pacific, North America, Europe, Latin America, the Middle East and Africa. The impact of these predictions reaches the economies (potentially any private and public institution or individual) of these zones.
The research in [1] is potentially a first work of many for adaptive SMC. The mathematical assumptions used to show the validity could be further refined to allow even more universality of the results. In addition, the ideas could be used to further develop new and even more powerful algorithms for large datasets.
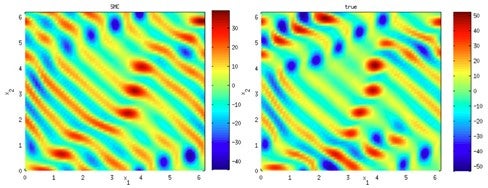
Figure shows the use of adaptive SMC for field estimation (used in weather prediction). The left is the true field and the right the estimated field by adaptive SMC. The algorithm which is used can be found in [4].
References
[1] Beskos, A., Jasra, A., Kantas, N. & Thiery A. “On the convergence of adaptive sequential Monte Carlo methods”. Annals of Applied Probability. 26 (2016) 1111-1146.
[2] Jasra, A., Stephens, D., Doucet A. & Tsagaris, T. “Inference for Lévy driven stochastic volatility
models via adaptive sequential Monte Carlo”. Scandinavian Journal of Statistics. 38 (2011) 1-22.
[3] Del Moral, P., Doucet, A. & Jasra A. “An adaptive sequential Monte Carlo method for approximate Bayesian Computation”. Statistics and Computing. 22 (2012) 1009-1020.
[4] Kantas, N., Beskos, A. & Jasra A. “SMC for inverse problems: A case study for the Navier Stokes Equation”. SIAM/ASA Journal on Uncertainty Quantification. 2 (2014) 464-489.


