Identities for punctured torus groups

26 Nov 2015 Mathematicians in NUS have discovered new variations to the McShane identity for SL(2,C) characters of the punctured torus group.

G. McShane discovered a remarkable identity for hyperbolic punctured tori involving a simple function of the lengths of the simple closed geodesics. This has been generalized from a geometric point of view in several different contexts, for example to hyperbolic surfaces with higher genus (with cusps, cone points or geodesic boundaries) by McShane [McS], Tan-Wong-Zhang [TWZ1], [TWZ2] and Mirzakhani [Mir] among others. The generalizations for the case of cone points or geodesic boundary do not limit to the original McShane identity, one has to take a derivative. In a recent paper Hu-Tan-Zhang [HTZ], a team led by Prof TAN Ser Peow from the Department of Mathematics in NUS found new variations of the McShane identity for SL(2,C) characters of the punctured torus group by utilizing a algebraic/combinatorial method. Their new variations in fact limit to the original McShane identity directly.

Mirzakhani used her variation of the McShane identities to prove important results on the Weil-Petersson volumes of the moduli spaces of bordered Riemann surfaces [Mir]. The new identities they found may also shed light on the geometry of the moduli spaces of Riemann surfaces, which is an important fundamental space which occurs in several different areas of mathematics including algebraic geometry, mathematical physics and hyperbolic geometry.

The identities they discovered are proven using algebraic/combinatorial methods. They would like to also have a good geometric interpretation and understanding of these identities and to generalize them to surfaces of higher genus. They are also looking into possible applications of the identities to the study of the geometry of the moduli spaces of Riemann surfaces and of character varieties in general.

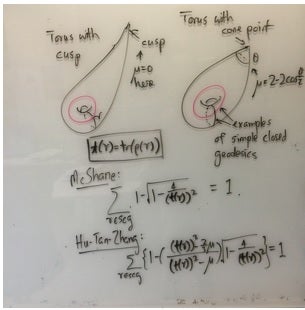
Comparisons of the McShane identity and the new identity for a torus with a cone point. [Image credit: Tan SP]

References

1. [HTZ] Hu H, Tan S, Zhang Y, “A new identity for SL(2,C)-characters of the once punctured torus group.” Math. Res. Lett., Volume 22, Number 2 (2015) 485.

2. [Mir] Mirzakhani M. “Simple geodesics and Weil-Petersson volumes of moduli spaces of bordered Riemann surfaces.” Invent. Math., 167 (2007) 179.

3. [McS] McShane G. “Simple geodesics and a series constant over Teichmuller Space.” Invent. Math., 132 (1998) 607.

4. [TWZ1] Tan S, Wong Y, Zhang Y, “Generalizations of McShane’s identity to hyperbolic cone-surfaces”, J. Differential Geom. 72 (2006), no. 1, 73.

5. [TWZ2] Tan S, Wong Y, Zhang Y, “Generalized Markoff maps and McShane’s identity”, Adv. Math. 217 (2008), no. 2, 761.