A team led by Prof YAO Zhigang from the Department of Statistics and Applied Probability in NUS is working with a space that carries the structure of a nonlinear manifold. A physical space where the data reside or an embedded space within the higher-dimensional data space introduces certain challenges [see Figure]. For example, in the analysis of temporal evolution of leaf shapes over a growing period, their shape spaces are modelled as manifolds on which transport along curves naturally qualifies as a measure for the similarity deformation. In order to capture the main direction of the leaf deformation, the dynamics of mean shape variation is of great interest.
Recently, they have developed a new approach for analyzing shape dynamics. The goal lies in the quantification of the same deformation of different shapes (e.g., leaf shapes), which is beyond the analysis of static shapes. The principal sub-manifold approach is motivated from the principal flow approach [1], the idea of which is to study the shapes from their low-dimensional embedding, rather than from their original high-dimensional sample space, which usually tends to be quite difficult.
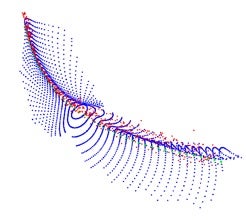
This figure shows a low-dimensional structure (in blue) from the high dimensional data (in red), with the principal direction of variation (in green) for the data; all of them have been projected to 3D for visualization purpose. [Image credit: Yao ZG]
Reference
Panaretos MV, Pham T, Yao Z. “Principal Flows.” Journal of the American Statistical Association. 109 (2014) 424.


