Identities for closed hyperbolic surfaces

1 Oct 2014. NUS mathematicians have derived new identities on the moduli space of closed hyperbolic surfaces.

Surfaces are some of the most basic and ubiquitous objects in mathematics. It has long been known that closed (no boundary), orientable (two-sided) surfaces are classified by their genus, for example the genus zero surface is a sphere, the genus one surface is a torus (“doughnut with one hole”), the genus two surface is a “doughnut with two holes” etc. (see Figure 1).

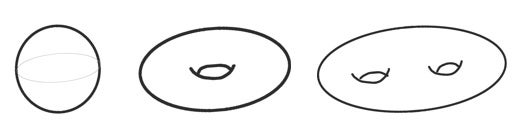
Figure 1 shows the surfaces of genus 0, 1 and 2. [Image credit: Tan SP]

It turns out that these surfaces admit metrics of constant curvature. For example, the torus admits a two dimensional family of Euclidean structures (flat metrics). These can be realized by identifying opposite sides of a parallelogram (normalized so that the area is 1). Hence the space of Euclidean structures on the torus is equivalent to the space of parallelograms of area one, these can be represented by points on the upper half plane. Surfaces of higher genus are the most interesting as they admit families of hyperbolic metrics, that is, metrics of constant negative curvature. Every point on these surfaces look like saddle points. More generally, surfaces with or without boundary of negative Euler characteristic admit families of hyperbolic structures, where the boundaries are restricted to be totally geodesic (straight). The dimension of the parameter space now depends on the genus of the surface and the number of boundary components. The space of such structures is called the moduli space. This space has a very rich geometry in itself and has been the subject of intense study over the years as it lies in the confluence of several areas of mathematics including Riemann surfaces, hyperbolic geometry, low dimensional topology, algebraic geometry, dynamical systems, number theory and mathematical physics.

A major challenge is to understand how the geometry of the underlying surface changes as one moves inside the moduli space. For example how do the lengths of closed geodesics change as the hyperbolic structure varies on the surface. In the last couple of decades, several identities have been discovered for hyperbolic surfaces with boundary, notably by Basmajian, McShane and Bridgeman. These identities involve infinite sums where each summand is indexed by a geometric object like an orthogeodesic (a geodesic arc intersecting the boundary perpendicularly at both ends), and is a function of some combination of the lengths of some simple closed geodesics or orthogeodesics. The identities provide some clues to the question above as it shows that as we vary the hyperbolic structures, the lengths of the various geometric objects must also vary in such a way that the identities remain valid. The (existence of the) boundary featured in an essential way in the derivation of these identities and for several years, there was a question of whether similar identities can be derived for surfaces without boundary.

Recently, Prof TAN Ser Peow from the Department of Mathematics in NUS, together with his co-author Prof Feng LUO from Rutgers, was able to do this using some new insights. They have derived some new identities on the moduli space of closed hyperbolic surfaces without boundary. These identities take the form

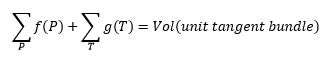
where the right hand side is the volume of the unit tangent bundle of the surface, and on the left hand side, the first sum is over all embedded geometric three-holed spheres P, and the second sum is over all embedded geometric one-holed tori T in the surface. Both of these sums are infinite sums and the functions and are dilogarithm functions defined on the lengths of the simple closed geodesics on the simple surfaces P and T.

The new identities have potential applications to the study of Riemann surfaces, Teichmüller Theory, Algebraic Geometry and Mathematical Physics.

Reference

F LUO, SP TAN. “A dilogarithm identity on moduli spaces of curves, J”. Differential Geom. 97 (2014) 255-274.