High-dimensional statistical problems
Ajay JASRA (Group Leader, Statistics and Applied Probability) () August 10, 201410 Aug 2014. NUS professors have demonstrated the feasibility of computational algorithms in high-dimensions.
In recent years, there has been an explosion of data in many applied disciplines such as in finance and genetics. As a result, the primary job of many statisticians has been to develop advanced stochastic models to capture these data. In these statistical models one is interested to estimate a variety of parameters and this is categorized by evaluating an integral (a mathematical object and gives a number), in very high-dimensions. To calculate this integral, one needs to use complex numerical methods and it is shown that an important algorithm provides reliable answers in reasonable time in high-dimensions.
Professor Ajay JASRA’s team from the Department of Statistics in NUS has helped to show that the algorithm, sequential Monte Carlo (SMC), has a computational cost that is polynomial in the dimension of the problem (see Figure). This allows it to be implemented on modern computing facilities. This is not previously known and the algorithm is thought to have exponential complexity – that is not implementable in practice. The main implication is that some of the most challenging statistical problems can be dealt with using the SMC algorithm, and the range of possible models used in practice, expanded. This means more realistic predictions and data analysis.
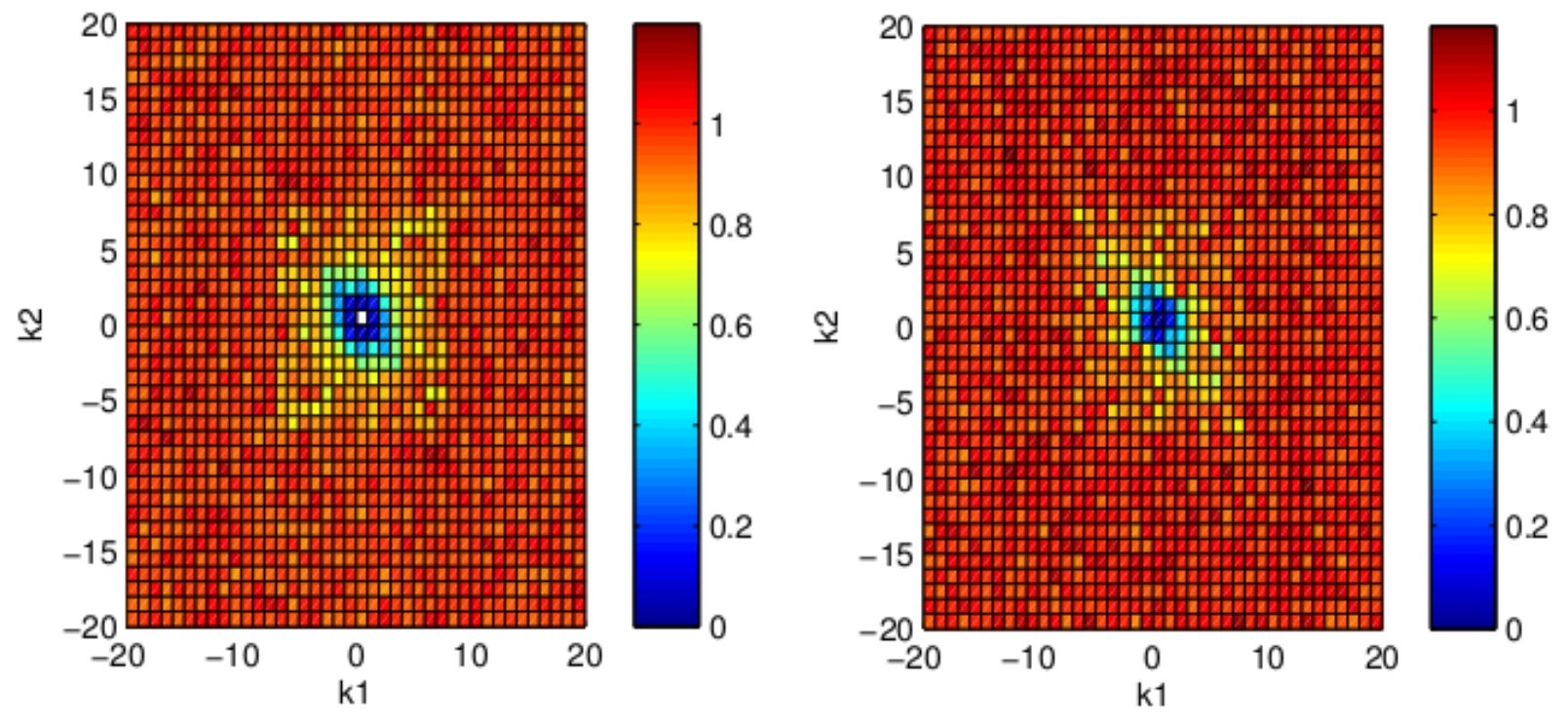
Image shows two summarized probability distributions from an SMC Algorithm. The problem is in over 4000 dimensions (Kantas et al, 2014). The distributions are associated to inferring the initial condition of the Navier Stokes equation, used for wind velocities in weather forecasting. (Picture credit: Ajay JASRA)
References
1. Beskos A, Crisan D, Jasra A. “On the stability of sequential Monte Carlo in high-dimensions.” Annals of Applied Probability. 24 (2014) 1396.
2. Kantas N, Beskos A, Jasra A. “Sequential Monte Carlo for High-Dimensional Inverse problems: A case study for the Navier Stokes equations.” SIAM/ASA Journal of Uncertainty Quantification. (In Preparation) (2014).


