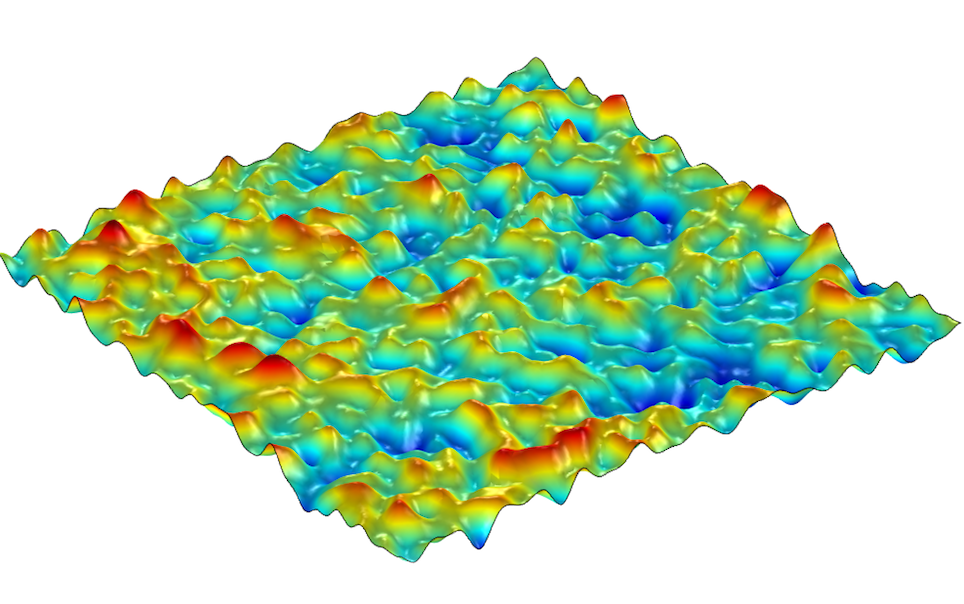
The critical 2d stochastic heat flow
Stochastic partial differential equations are used to describe many physical phenomena involving randomness, such as the evolution of the front of a forest fire or diffusion in random media. However, many of these equations are not mathematically well-defined. In a recent breakthrough with his coauthors, Prof SUN Rongfeng constructed a stochastic process, called the critical two-dimensional (2D) stochastic heat flow, which gives meaning to the long-sought solution of the stochastic heat equation in the critical dimension 2 and in the critical window where a phase transition occurs. This study was published in Inventiones mathematicae (March 2023).
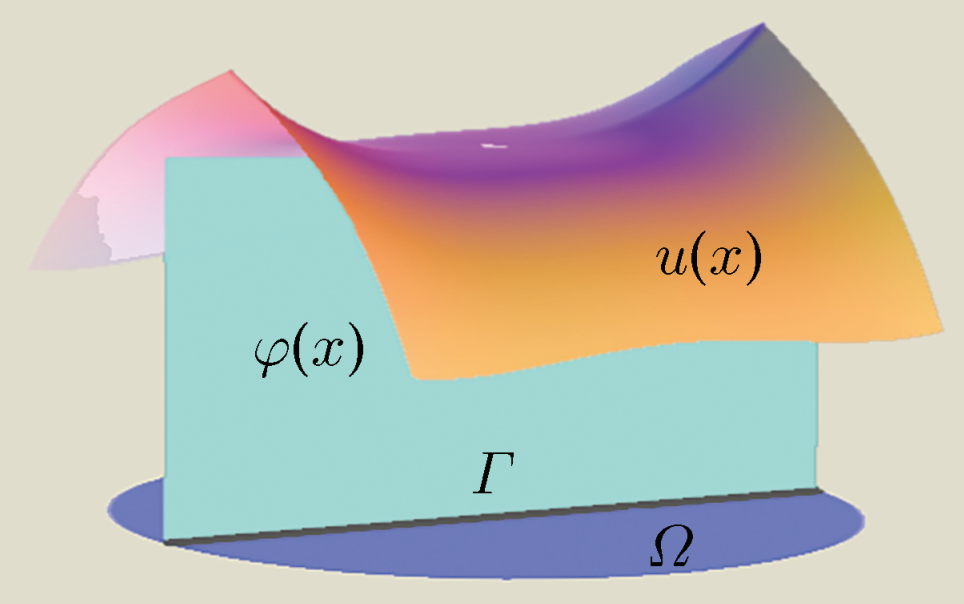
Regularity of the singular set in nonlinear free boundary problems
Many natural phenomena, for instance, glaciers in the ocean, involve multiple phases. It is important to address properties of the interface separating the phases. Previously, the study of free boundary problems was restricted to situations governed by linear equations. Together with his collaborators, Asst Prof YU Hui designed a new strategy which allows the study of nonlinear problems. They achieved the same results for the obstacle problem, a problem arising in multiplayer games as in linear theory. Their work has inspired many studies on related nonlinear problems and was published in the Journal of the European Mathematical Society (March 2023).












