Fast algorithms for quantifying uncertainty
David NOTT ((Group Leader, Statistics and Applied Probability) ) January 19, 201719 Jan 2017. NUS statisticians have developed a method to estimate unknown parameters efficiently for modelling complex situations.
Statistical models which attempt to describe the processes involved in the generation of complex data are widely used for understanding variability in experiments and observational studies and other crucial real world tasks such as forecasting. Generally these complex models have unknown parameters in them that need to be estimated from observed data. The process of estimation of parameters and quantifying uncertainties in this process is important and difficult.
A common approach to the problem uses Bayesian inference. In this method, a probabilistic model is set up for the unknown quantities we wish to learn about together with the data that is to be observed and then the laws of conditional probability allow us to quantify uncertainties about the unknowns after observing the data. Although Bayesian inference is attractive in principle, one difficulty with it is the computations that are required for implementing the method. One approximate method for implementing the required computations is variational approximation; this formulates the required computation as an optimization problem.
Variational approximation methods currently are difficult to apply when the unknowns to be estimated are very high dimensional (involve many parameters), because the required optimisation occurs in a very high-dimensional space. Recent work by researchers in the Department of Statistics and Applied Probability at NUS, Dr Linda TAN and Prof David NOTT, has been concerned with using the structure of the model to reduce the dimensionality of the optimization required. The method exploits sparsity in the dependence structure of the approximating distributions in the method. It allows crucial uncertainty quantifications in complex models to be done quickly even when the unknowns of interest are very high-dimensional.
The methods developed also have the potential to be combined with other techniques for reducing the number of variational parameters in the approach, resulting in an attractive framework for fast approximate inference in complex models.
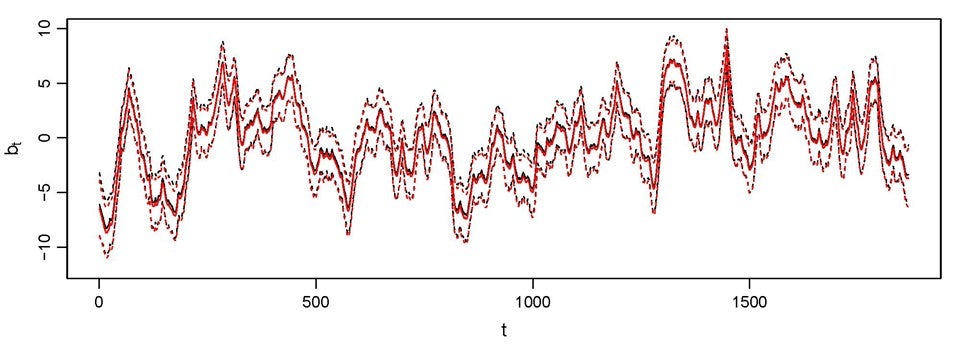
Figure shows the estimation of volatility parameter in a model for financial time series data via exact (black) and the proposed approximate (red) inference methods.
Reference
Tan Linda S-L; Nott David J., “Gaussian variational approximation with sparse precision matrix” https://arxiv.org/abs/1605.05622. (2016)


