What is the weather tomorrow?

26 Jul 2017. NUS mathematician has revealed ways which can lead to more accurate weather predictions.

Weather forecasting is one of the most computationally challenging problems in science. Forecasts are produced by simulating a numerical model of the Earth’s weather patterns and then predicting its future behaviours. For such simulations to correctly reflect actual weather conditions with high accuracy, it is important to update the model with the latest satellite data. This is an extremely challenging problem, where billions of model components that can affect the weather are involved. Fortunately, there are advanced mathematical structures which can be used to simplify this task.

Computational power available today can process several hundred simulations at one time. According to classical mathematical theory, this would not be sufficient to accurately simulate the complexities of the Earth model. Interestingly, weather forecasts made today can be quite accurate. This is made possible by using an algorithm known as the ensemble Kalman filter (EnKF), which performs well for this task. Such stark contrast between theory and reality is mystifying. Prof TONG Xin from the Department of Mathematics, NUS in collaboration with Prof Andrew MAJDA from New York University, are studying this phenomenon and have shown that the predictive power of EnKF may come from a systematic low effective dimensionality and localisation structure.

The ensemble Kalman filter (EnKF) (see Figure 1) is a popular computational method for weather forecasting. Existing theoretical studies of the EnKF consider mostly the low dimension-large sample size scenario, in which there is a large number of samples with few model components. Unfortunately, the situation is often reversed in real-life applications.  This makes existing theory difficult to improve the performance of existing EnKF algorithms for practical scenarios. In order to resolve this issue, two model structures are investigated: a low effective dimension and a localisation covariance (see Figure 2). While these structures were identified heuristically before, a rigorous justification requires knowledge of advanced statistics, dynamical system and control theory.

This research lays the mathematical foundation for the use of EnKF in high dimensions for selected applications. It provides the fundamental conditions in which EnKF can operate effectively. Armed with these latest findings, new EnKF algorithms with improved accuracy can be developed for selected applications. For example, one important issue for EnKF application is the optimisation of an algorithmic parameter, known as the localisation radius. This problem was studied previously only by trial and error. The results by Prof Tong provide a new theoretical perspective for this problem, enabling users to develop guidelines for determining the localisation parameters.

Despite the fact that EnKF was derived in a linear setting, it works very well with nonlinear models in practice. The current research outcomes from this work are conducted only for linear models and would need to be expanded to cover nonlinear models so as to be able to understand and tap the full potential of EnKF.

Prof Tong said, “Linear and nonlinear problems are vastly different in theory. The former can be efficiently solved even in high dimensions, while the latter is the opposite. However, we see in practice that many nonlinear problems can be solved using linear methods. EnKF is one good example. The reasons behind await our further exploration.”

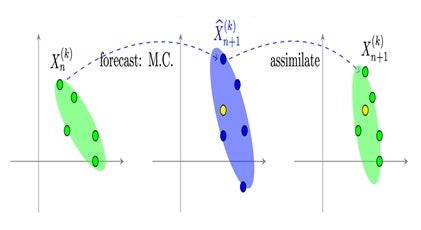
Figure 1 shows an illustration of the ensemble Kalman filter concept. Each green dot represents a possible estimate of earth atmosphere at a given time. Forecast simulations, represented by blue dots, are produced based on previous estimates. Then the current satellite image, represented a yellow dot, is assimilated to adjust the forecasts into more accurate estimates.

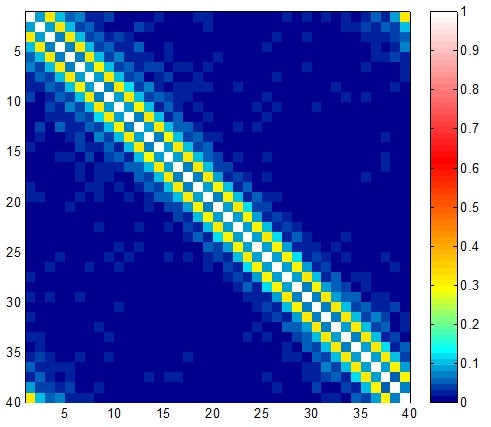
Figure 2 shows a correlation localisation pattern between components. The component correlation of a 40-dimensional nonlinear turbulent model, the Lorenz 96, is plotted above. Although the dynamics of this model are complicated and nonlinear, the plot shows an obvious correlation (diagonal line pattern). In particular, components which are located away from the diagonal line are close to being independent.

References

Majda AJ; Tong XT*, “Performance of Ensemble Kalman filters in large dimensions” COMMUNICATIONS ON PURE AND APPLIED MATHEMATICS Accepted: 2017.

Kelly D; Majda AJ; Tong XT*, “Nonlinear stability and ergodicity of ensemble based Kalman filters” NONLINEARITY Volume: 29 Issue: 2 Pages: 657-691 DOI: 10.1088/0951-7715/29/2/657 Published: 2016.

Kelly D; Majda AJ; Tong XT*, ” Concrete ensemble Kalman filters with rigorous catastrophic filter divergence” PROCEEDINGS OF THE NATIONAL ACADEMY OF SCIENCES OF THE UNITED STATES OF AMERICA Volume: 112 Issue: 34 Pages: 10589-10594 DOI: 10.1073/pnas.1511063112 Published: 2015.